ImagePath Module

class Path

compact

doc

https://pillow.readthedocs.io/en/latest/reference/ImagePath.html#PIL.ImagePath.PIL.ImagePath.Path.compact, http://effbot.org/imagingbook/imagepath.htm#tag-ImagePath.Path.compact

import math from PIL import ImagePath def _create_demo_imgs(xy, size): # to clarify behaviour of compact method, # this demo shows up 'line' version and # 'point' version. from PIL import Image, ImageDraw imgp = Image.new("L", size, color=240) dctx = ImageDraw.Draw(imgp) dctx.point(xy) del dctx imgl = Image.new("L", size, color=240) dctx = ImageDraw.Draw(imgl) dctx.line(xy) del dctx return imgp, imgl def _save_result(imgs, outfilepath): # drawing single point on large canvas is not visible # for human's eye, so this demo use very small canvas # and later resize it. size = (imgs[0].width * 8, imgs[0].height * 8) imgs[0].resize(size).save(outfilepath + "p.jpg") imgs[1].resize(size).save(outfilepath + "l.jpg") # xy = [] for x in range(0, 32, 4): xy.extend([ (x, x // 4 * 2), (x + 2, x // 4 * 2), (x + 4, x // 4 * 2)]) # calculate bounding box bb = list(map(int, map(math.ceil, ImagePath.Path(xy).getbbox()))) # with original xy imgs = _create_demo_imgs(xy, bb[2:]) _save_result(imgs, "result/ImagePath_compact_01_1") # compact(distance=4) xy_c = ImagePath.Path(xy) xy_c.compact(4) # This method modifies the path in place, # and returns the number of points left # in the path. # distance is measured as Manhattan distance # (https://en.wikipedia.org/wiki/Taxicab_geometry) # and defaults to two pixels. imgs = _create_demo_imgs(xy_c, bb[2:]) _save_result(imgs, "result/ImagePath_compact_01_2") # compact(distance=4 + 2) xy_c = ImagePath.Path(xy) xy_c.compact(4 + 2) imgs = _create_demo_imgs(xy_c, bb[2:]) _save_result(imgs, "result/ImagePath_compact_01_3")

original compact(distance=4) compact(distance=6)

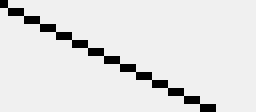import numpy as np
from PIL import Image, ImagePath, ImageDraw

# epicycloid
rc, rm = 5, 1
th = np.linspace(0, 2 * np.pi, 360)
X = (rc + rm) * np.cos(th) - rm * np.cos(((rc + rm) / rm) * th)
Y = (rc + rm) * np.sin(th) - rm * np.sin(((rc + rm) / rm) * th)
X = (X - X.min()) * 30
Y = (Y - Y.min()) * 30

#
xy = list(zip(X, Y))
ipath = ImagePath.Path(xy)
bb = list(map(int, map(np.ceil, ipath.getbbox())))

# original path
img = Image.new("RGB", bb[2:], color="#f0f0ff")
dctx = ImageDraw.Draw(img)
dctx.line(ipath, fill="blue")
del dctx
img.save("result/ImagePath_compact_02_0.jpg")

# compact (repeat)
for i in range(5):
    img = Image.new("RGB", bb[2:], color="#f0f0ff")
    dctx = ImageDraw.Draw(img)
    ipath.compact((i + 1) * 15)  # modifies the path in place
    dctx.line(ipath, fill="blue")
    del dctx
    img.save("result/ImagePath_compact_02_%d.jpg" % i)

original

compact

more compact

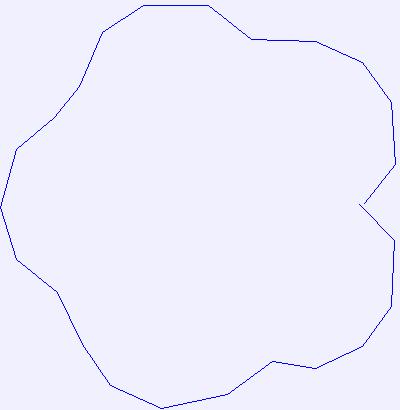more compact

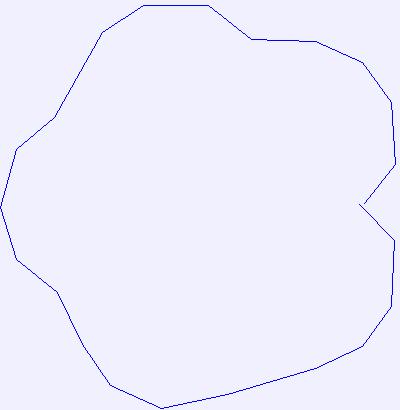more compact

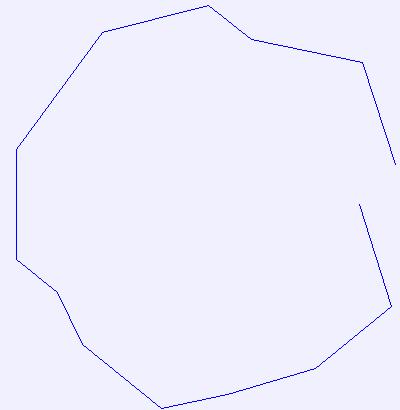getbbox

doc

https://pillow.readthedocs.io/en/latest/reference/ImagePath.html#PIL.ImagePath.PIL.ImagePath.Path.getbbox, http://effbot.org/imagingbook/imagepath.htm#tag-ImagePath.Path.getbbox

>>> import math
>>> from PIL import ImagePath
>>> # integers
... xy = list(zip(range(3, 10, 1), range(24, 5, -2)))
>>> xy
[(3, 24), (4, 22), (5, 20), (6, 18), (7, 16), (8, 14), (9, 12)]
>>> bb = ImagePath.Path(xy).getbbox()
>>> bb
(3.0, 12.0, 9.0, 24.0)
>>> list(map(int, bb))
[3, 12, 9, 24]
>>> # floating points
... xy = list(zip([i / 4. for i in range(3, 10, 1)], [i / 2. for i in range(24, 5, -2)]))
>>> xy
[(0.75, 12.0), (1.0, 11.0), (1.25, 10.0), (1.5, 9.0), (1.75, 8.0), (2.0, 7.0), (2.25, 6.0)]
>>> bb = ImagePath.Path(xy).getbbox()
>>> bb
(0.75, 6.0, 2.25, 12.0)
>>> list(map(int, map(math.floor, bb[:2])))  # (left, top)
[0, 6]
>>> list(map(int, map(math.ceil, bb[2:])))  # (right, bottom)
[3, 12]

map

doc

https://pillow.readthedocs.io/en/latest/reference/ImagePath.html#PIL.ImagePath.PIL.ImagePath.Path.map, http://effbot.org/imagingbook/imagepath.htm#tag-ImagePath.Path.map

>>> from PIL import ImagePath
>>> xy = list(zip(range(3, 8, 1), range(22, 5, -2)))
>>> xy
[(3, 22), (4, 20), (5, 18), (6, 16), (7, 14)]
>>> aspath = ImagePath.Path(xy)
>>> aspath.tolist()
[(3.0, 22.0), (4.0, 20.0), (5.0, 18.0), (6.0, 16.0), (7.0, 14.0)]
>>> # map method modifies the path in place,
... aspath.map(lambda x, y: (x * 2, y * 3))
>>> aspath.tolist()
[(6.0, 66.0), (8.0, 60.0), (10.0, 54.0), (12.0, 48.0), (14.0, 42.0)]
>>> def _fun(x, y):
...     return (x - 10, y - 30)
...
>>> aspath.map(_fun)  # map method modifies the path in place,
>>> aspath.tolist()
[(-4.0, 36.0), (-2.0, 30.0), (0.0, 24.0), (2.0, 18.0), (4.0, 12.0)]

tolist

doc

https://pillow.readthedocs.io/en/latest/reference/ImagePath.html#PIL.ImagePath.PIL.ImagePath.Path.tolist, http://effbot.org/imagingbook/imagepath.htm#tag-ImagePath.Path.tolist

>>> from PIL import ImagePath
>>> xy = list(zip(range(3, 8, 1), range(22, 5, -2)))
>>> xy
[(3, 22), (4, 20), (5, 18), (6, 16), (7, 14)]
>>> aspath = ImagePath.Path(xy)
>>> aspath.tolist()
[(3.0, 22.0), (4.0, 20.0), (5.0, 18.0), (6.0, 16.0), (7.0, 14.0)]
>>> aspath.tolist(True)
[3.0, 22.0, 4.0, 20.0, 5.0, 18.0, 6.0, 16.0, 7.0, 14.0]

transform

doc

https://pillow.readthedocs.io/en/latest/reference/ImagePath.html#PIL.ImagePath.PIL.ImagePath.Path.transform, http://effbot.org/imagingbook/imagepath.htm#tag-ImagePath.Path.transform

import math from PIL import Image, ImagePath, ImageDraw xy = [ (0, 0), # box with diagonal ( 50, 100), # left, top (160, 100), # right, top (160, 150), # right, bottom ( 50, 150), # left, bottom ( 50, 100), # left, top (160, 150), # right, bottom ] # ipath = ImagePath.Path(xy) bb = (0, 0, 210, 160) # original path img1 = Image.new("RGB", bb[2:], color="#f0f0ff") dctx = ImageDraw.Draw(img1) dctx.line(ipath, fill="blue") del dctx img1.save("result/ImagePath_transform_01_0.jpg") # affine transform theta = math.pi / 15. ipath.transform(( math.cos(theta), math.sin(theta), 20, -math.sin(theta), math.cos(theta), 20, )) img2 = Image.new("RGB", bb[2:], color="#f0f0ff") dctx = ImageDraw.Draw(img2) dctx.line(ipath, fill="blue") del dctx img2.save("result/ImagePath_transform_01_1.jpg")

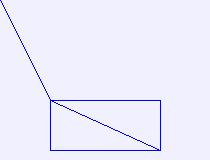orig

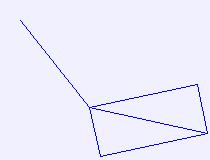affine transform