(ffmpeg-utils)3. Expression Evaluation (2)

doc

Expression Evaluation

see also

(ffmpeg-utils)3. Expression Evaluation

On this page, I’m going to write an expression that isn’t built into ffmpeg but can be written using it. However, there is no clear policy for collection, so what will be gathered here will be unorganized.

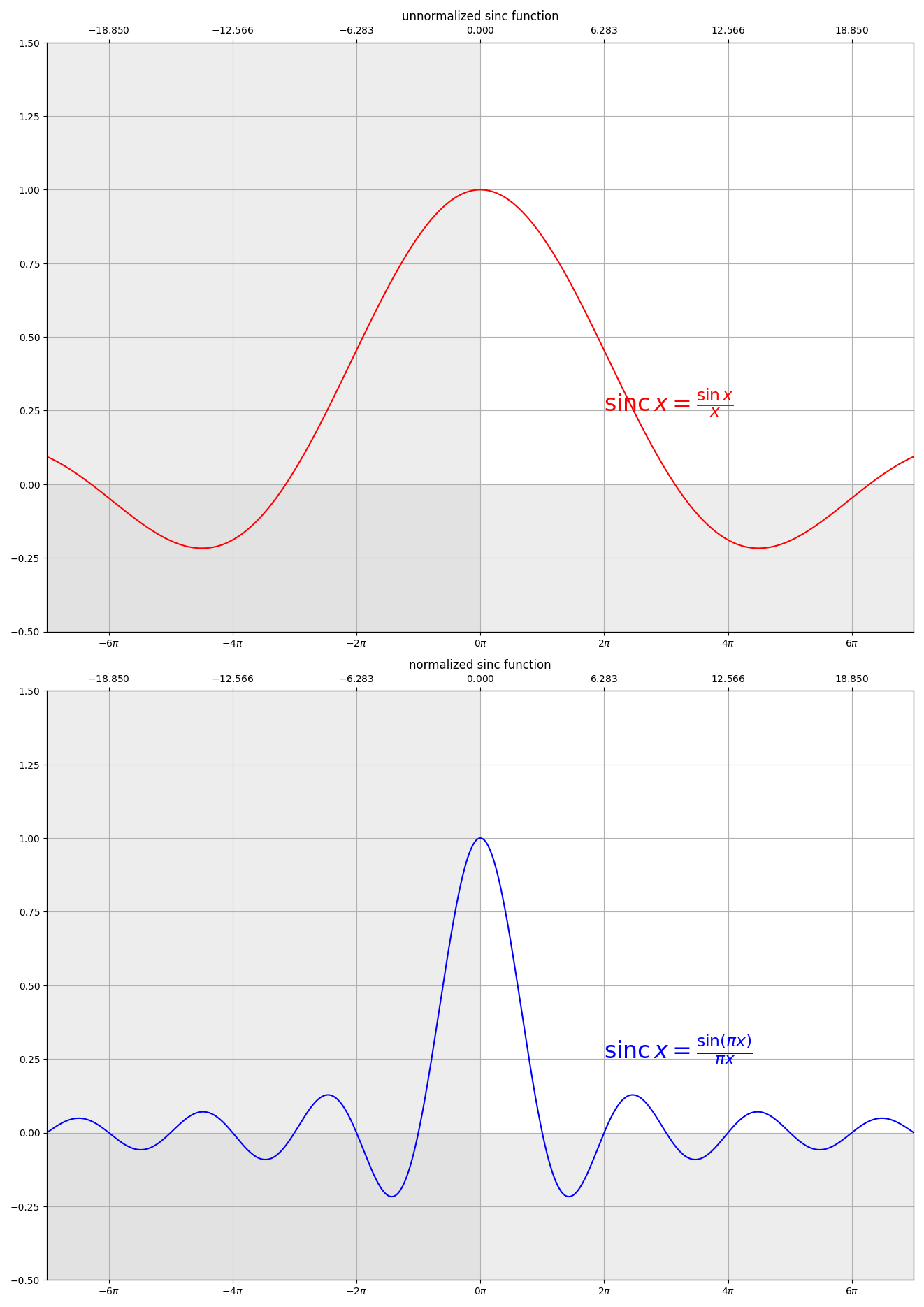
sinc(x)

unnormalized sinc function:

\[\operatorname{sinc}x = \frac{\sin x}{x}\]

normalized sinc function:

\[\operatorname{sinc}x = \frac{\sin(\pi x)}{\pi x}\]

[me@host: ~]$ # use sinc function as amplitude
[me@host: ~]$ ffplay -f lavfi "
> aevalsrc='
>     st(0, 4 - mod(t * PI, 8)) ;
>     0.5 * (sin(ld(0)) / ld(0)) * sin(220 * 2 * PI * t)'"

[me@host: ~]$ # use sinc function as frequency
[me@host: ~]$ ffplay -f lavfi "
> aevalsrc='
>     st(0, 4 - mod(t * PI, 8)) ;
>     0.5 * sin(220 * (sin(ld(0)) / ld(0)) * 2 * PI * t)'"

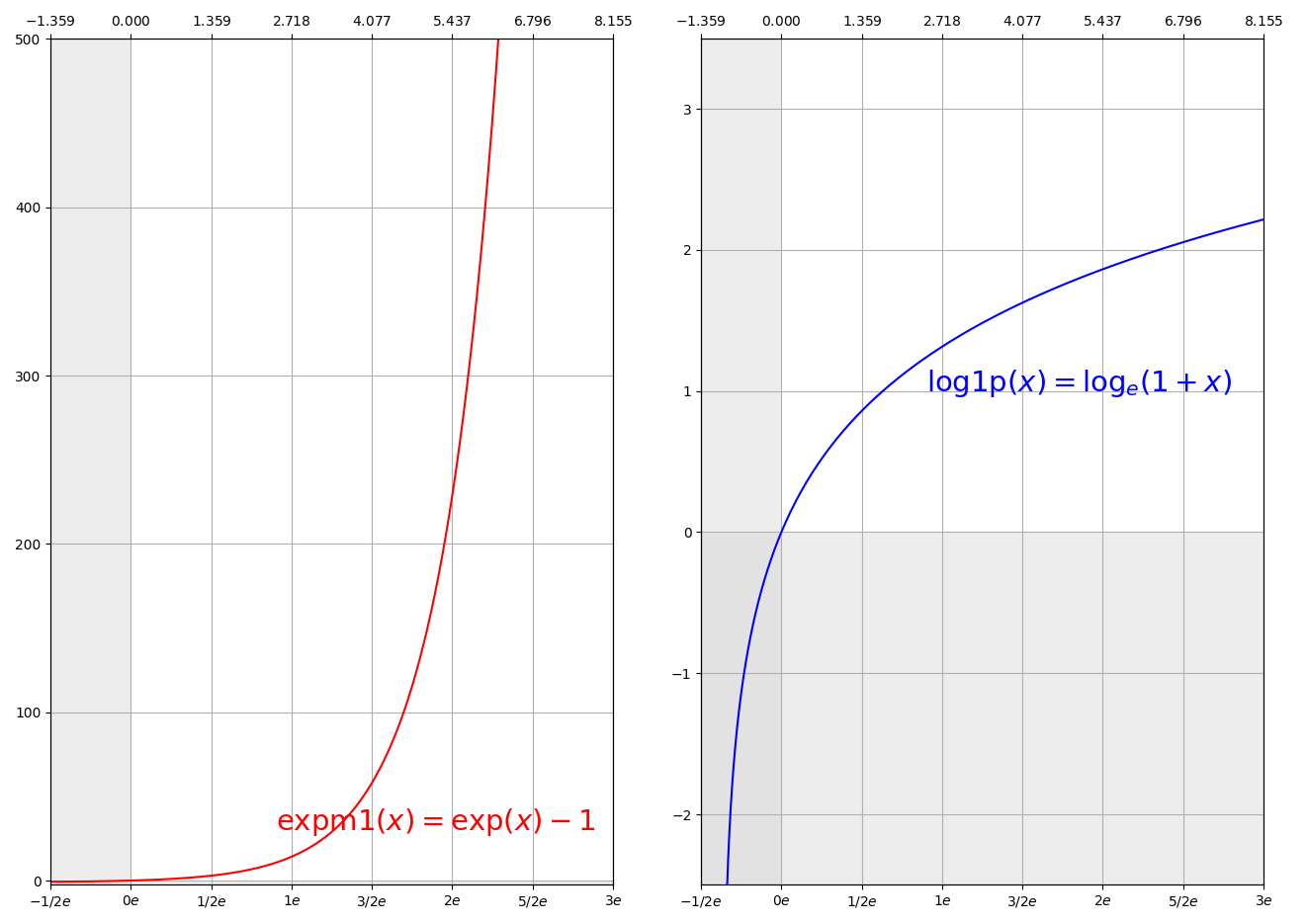
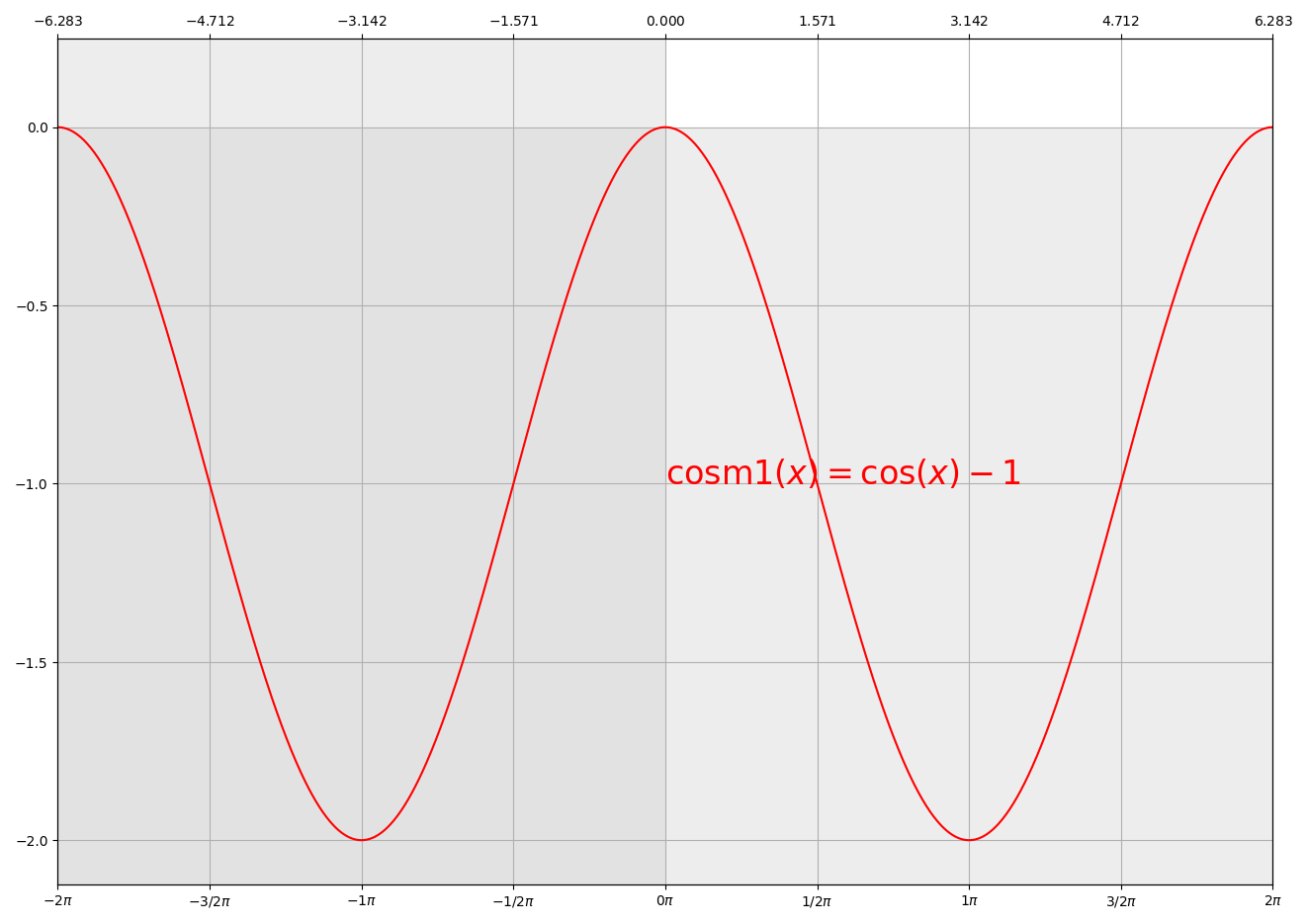
expm1(x), log1p(x), cosm1(x)

expm1(x) calculates \(\exp(x) - 1\), log1p(x) calculates expm1(x)’s inverse \(\log_{e}(1 + x)\), and cosm1(x) calculates \(\cos(x) - 1\):

Note

Note that this direct evaluation may differ from the result of the dedicated function that your favorite language provides. For example, ‘expm1’ which is provided by a modern standard C library avoids the loss of precision for small x.

lcm(x, y)

The least common multiple of x and y:

\[\operatorname{lcm}(x, y) = \frac{|xy|}{\gcd(x, y)}\]

[me@host: ~]$ # the least common multiple of 64 and 36 is 576.
[me@host: ~]$ ffplay -vf "scale=-1:'abs(64) / gcd(64, 36) * abs(36)'" video.mkv

see also

gcd(x, y)

dim(x, y)

Dim returns the maximum of x - y or 0:

\[\operatorname{dim}(x, y) = \operatorname{max}\left(0, x - y\right)\]

[me@host: ~]$ ffplay -vf "pad='1280:720:max(0,(ow-iw))/2:max(0,(oh-ih))/2'" video.mkv

see also

clip(x, min, max), max(x, y), min(x, y)

Window functions

It’s unlikely that you’ll use the window function in a filter graph for its intended purpose, but you might expect just the shape of the graph, for example to generate sound waveforms.

bartlett(n, M)

\[w(n) = \frac{2}{M - 1} \left( \frac{M - 1}{2} - \left|n - \frac{M - 1}{2}\right| \right)\]

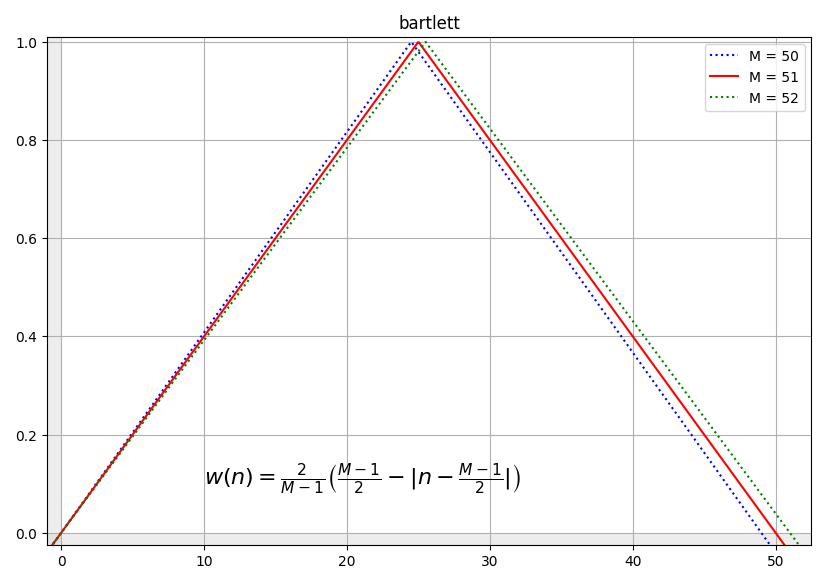
[me@host: ~]$ # use bartlett function as amplitude (M=11)
[me@host: ~]$ ffplay -f lavfi "
> aevalsrc='
>     st(0, 2 / (11 - 1)) ;
>     st(1, 1 / ld(0)) ;
>     0.5 * (ld(0) * (ld(1) - abs(t - ld(1)))) * sin(440 * 2 * PI * t)':d=10" -autoexit

hanning(n, M)

\[w(n) = 0.5 - 0.5cos\left(\frac{2\pi{n}}{M-1}\right) \qquad 0 \leq n \leq M-1\]

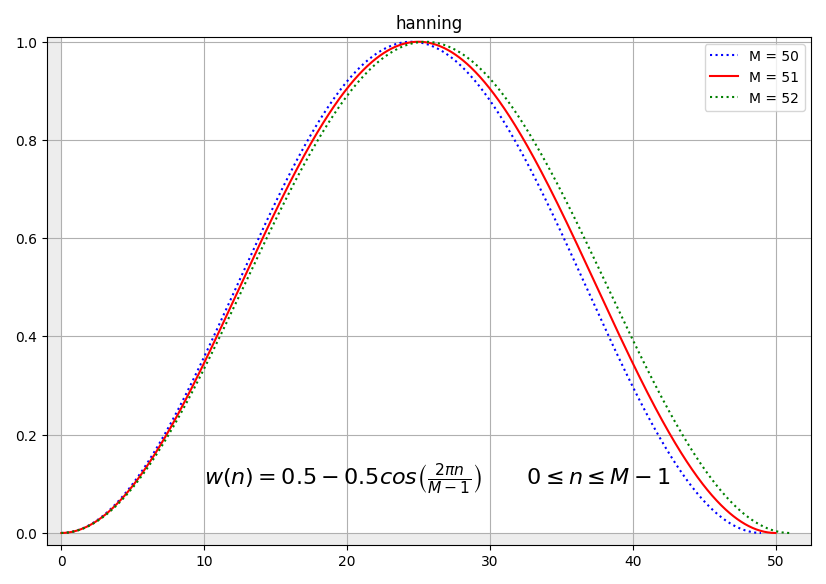
[me@host: ~]$ # use hanning function as amplitude (M=11)
[me@host: ~]$ ffplay -f lavfi "
> aevalsrc='
>     0.5 * (
>         0.5 - 0.5 * cos(2 * PI * t / (11 - 1))
>     ) * sin(440 * 2 * PI * t)':d=10" -autoexit

hamming(n, M)

\[w(n) = 0.54 - 0.46cos\left(\frac{2\pi{n}}{M-1}\right) \qquad 0 \leq n \leq M-1\]

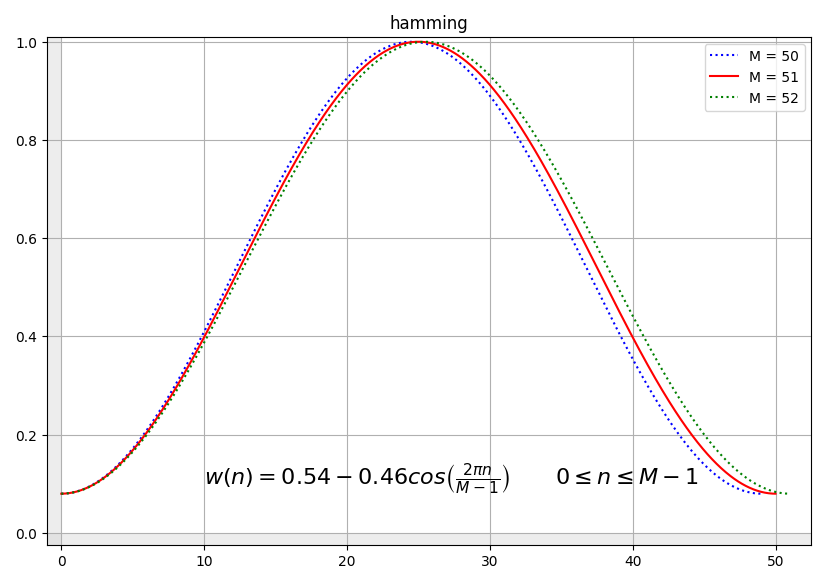
[me@host: ~]$ # use hamming function as amplitude (M=11)
[me@host: ~]$ ffplay -f lavfi "
> aevalsrc='
>     0.5 * (
>         0.54 - 0.46 * cos(2 * PI * t / (11 - 1))
>     ) * sin(440 * 2 * PI * t)':d=10" -autoexit

blackman(n, M)

\[w(n) = 0.42 - 0.5 \cos(2\pi n/M) + 0.08 \cos(4\pi n/M)\]

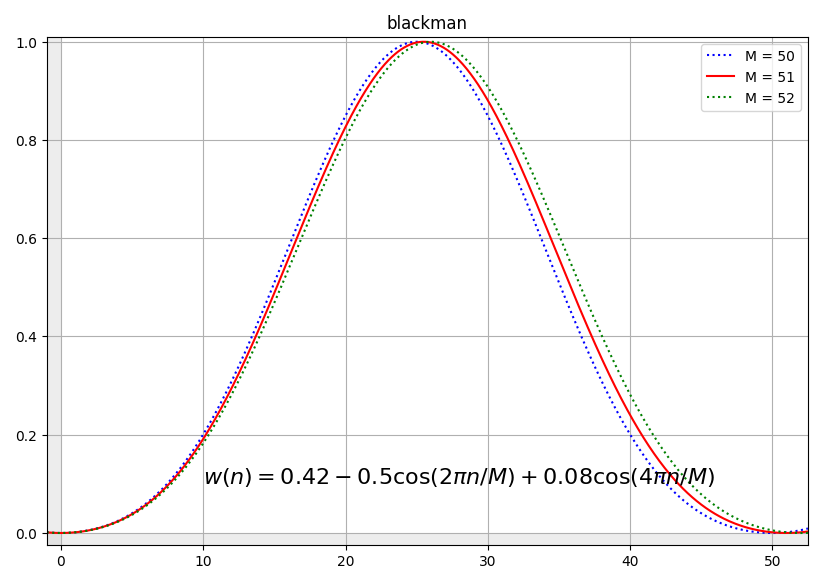
[me@host: ~]$ # use blackman function as amplitude (M=11)
[me@host: ~]$ ffplay -f lavfi "
> aevalsrc='
>     st(0, 2 * PI * t / 11) ;
>     0.5 * (
>         0.42 - 0.5 * cos(ld(0)) + 0.08 * cos(2 * ld(0))
>     ) * sin(440 * 2 * PI * t)':d=10" -autoexit