(ffmpeg-utils)3. Expression Evaluation

doc

Expression Evaluation

see also

(ffmpeg-utils)3. Expression Evaluation (2)

Official documentation says:

When evaluating an arithmetic expression, FFmpeg uses an internal formula evaluator, implemented through the libavutil/eval.h interface.

An expression may contain unary, binary operators, constants, and functions.

Two expressions expr1 and expr2 can be combined to form another expression "expr1;expr2". expr1 and expr2 are evaluated in turn, and the new expression evaluates to the value of expr2.

The following binary operators are available: +, -, *, /, ^.

The following unary operators are available: +, -.

Constants

  • PI

    area of the unit disc, approximately 3.14

  • E

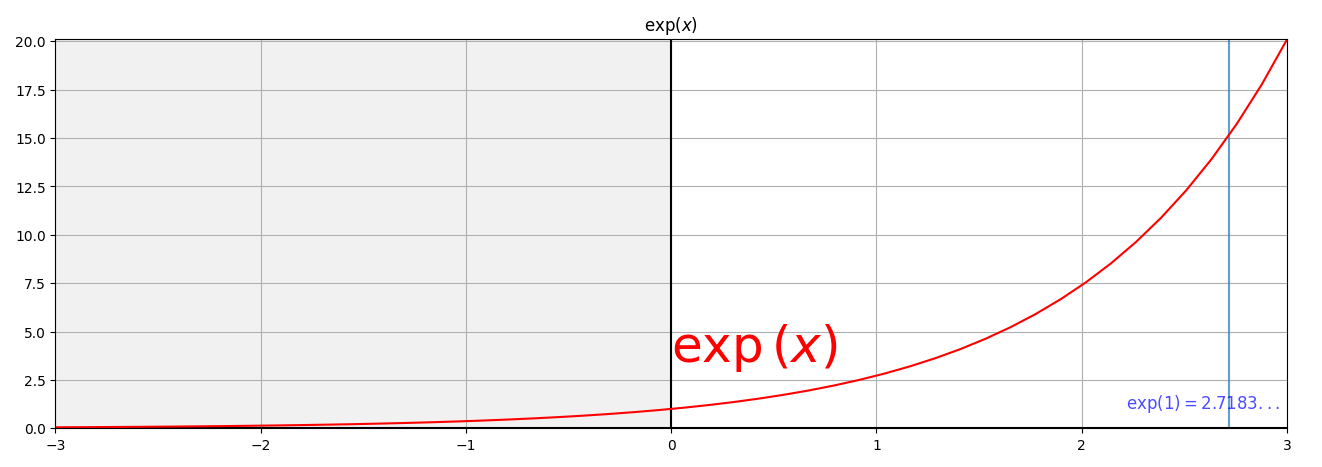
    \(\exp(1)\) (Euler’s number), approximately 2.718

  • PHI

    golden ratio \((1 + \sqrt{5}) / 2\), approximately 1.618

Functions

Logical functions

Official documentation says:

if(x, y)

Evaluate x, and if the result is non-zero return the result of the evaluation of y, return 0 otherwise.

if(x, y, z)

Evaluate x, and if the result is non-zero return the evaluation result of y, otherwise the evaluation result of z.

ifnot(x, y)

Evaluate x, and if the result is zero return the result of the evaluation of y, return 0 otherwise.

ifnot(x, y, z)

Evaluate x, and if the result is zero return the evaluation result of y, otherwise the evaluation result of z.

not(expr)

Return 1.0 if expr is zero, 0.0 otherwise.

.

between(x, min, max)

Return 1 if x is greater than or equal to min and lesser than or equal to max, 0 otherwise.

eq(x, y)

Return 1 if x and y are equivalent, 0 otherwise.

gt(x, y)

Return 1 if x is greater than y, 0 otherwise.

gte(x, y)

Return 1 if x is greater than or equal to y, 0 otherwise.

lt(x, y)

Return 1 if x is lesser than y, 0 otherwise.

lte(x, y)

Return 1 if x is lesser than or equal to y, 0 otherwise.

.

isinf(x)

Return 1.0 if x is +/-INFINITY, 0.0 otherwise.

isnan(x)

Return 1.0 if x is NAN, 0.0 otherwise.

Ffmpeg does not claim “confusing logical values and numbers is catastrophically dangerous” as in some modern programming languages. So, you can mix the results of logical values into the arithmetic operations as they are:

[me@host: ~]$ ffplay video.mkv -af "volume='lte(t, 2) * 0.1 + gt(t, 2)':eval=frame"

bitand(x, y), bitor(x, y)

Official documentation says:

bitand(x, y), bitor(x, y)

Compute bitwise and/or operation on x and y.

The results of the evaluation of x and y are converted to integers before executing the bitwise operation.

Note that both the conversion to integer and the conversion back to floating point can lose precision. Beware of unexpected results for large numbers (usually \(2^{53}\) and larger).

[me@host: ~]$ # The following two will have the same result:
[me@host: ~]$ ffplay video.mkv -vf "lutyuv=y='bitand(val, 0xF0)'"
[me@host: ~]$ ffplay video.mkv -vf "lutyuv=y='val - mod(val, 0x10)'"

Trigonometric functions

Official documentation says:

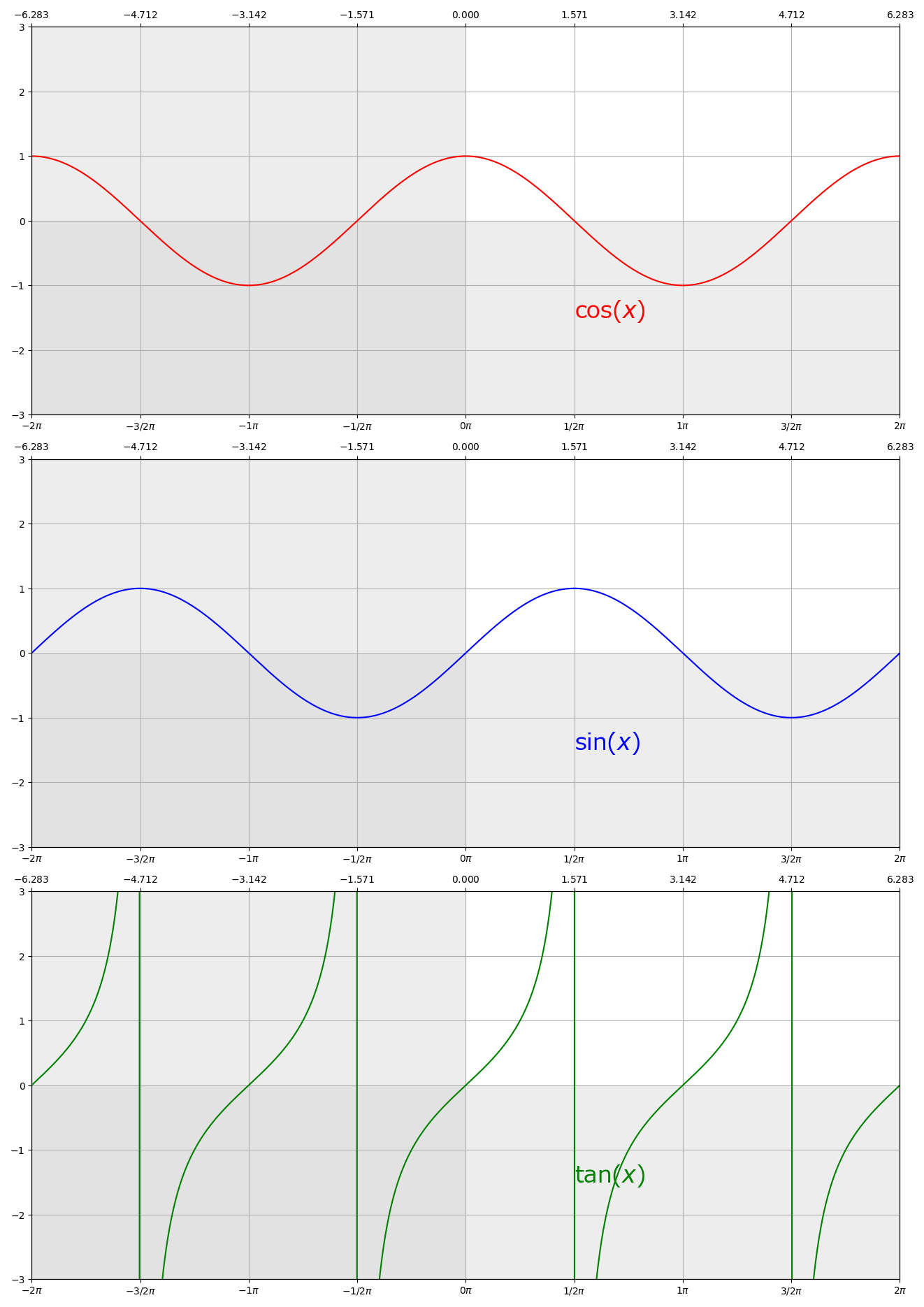
cos(x)

Compute cosine of x.

sin(x)

Compute sine of x.

tan(x)

Compute tangent of x.

../_images/expression_trig_graph.png 
[me@host: ~]$ ffplay -f lavfi "aevalsrc='0.5 * sin(440 * 2 * PI * t)'"
[me@host: ~]$ ffplay -f lavfi "aevalsrc='0.5 * cos(20 * t) * sin(440 * 2 * PI * t)'"

Inverse trigonometric functions

Official documentation says:

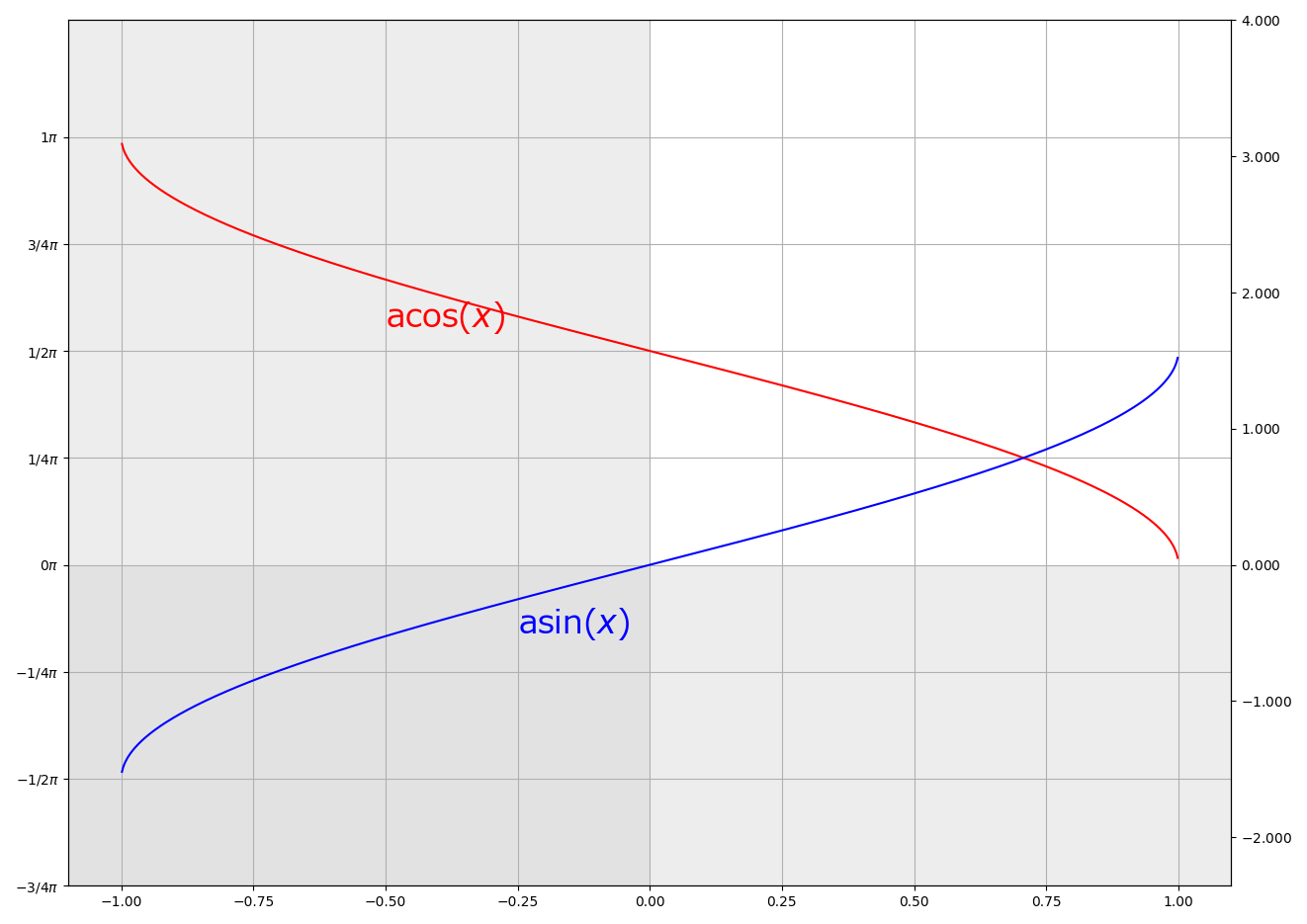
acos(x)

Compute arccosine of x.

asin(x)

Compute arcsine of x.

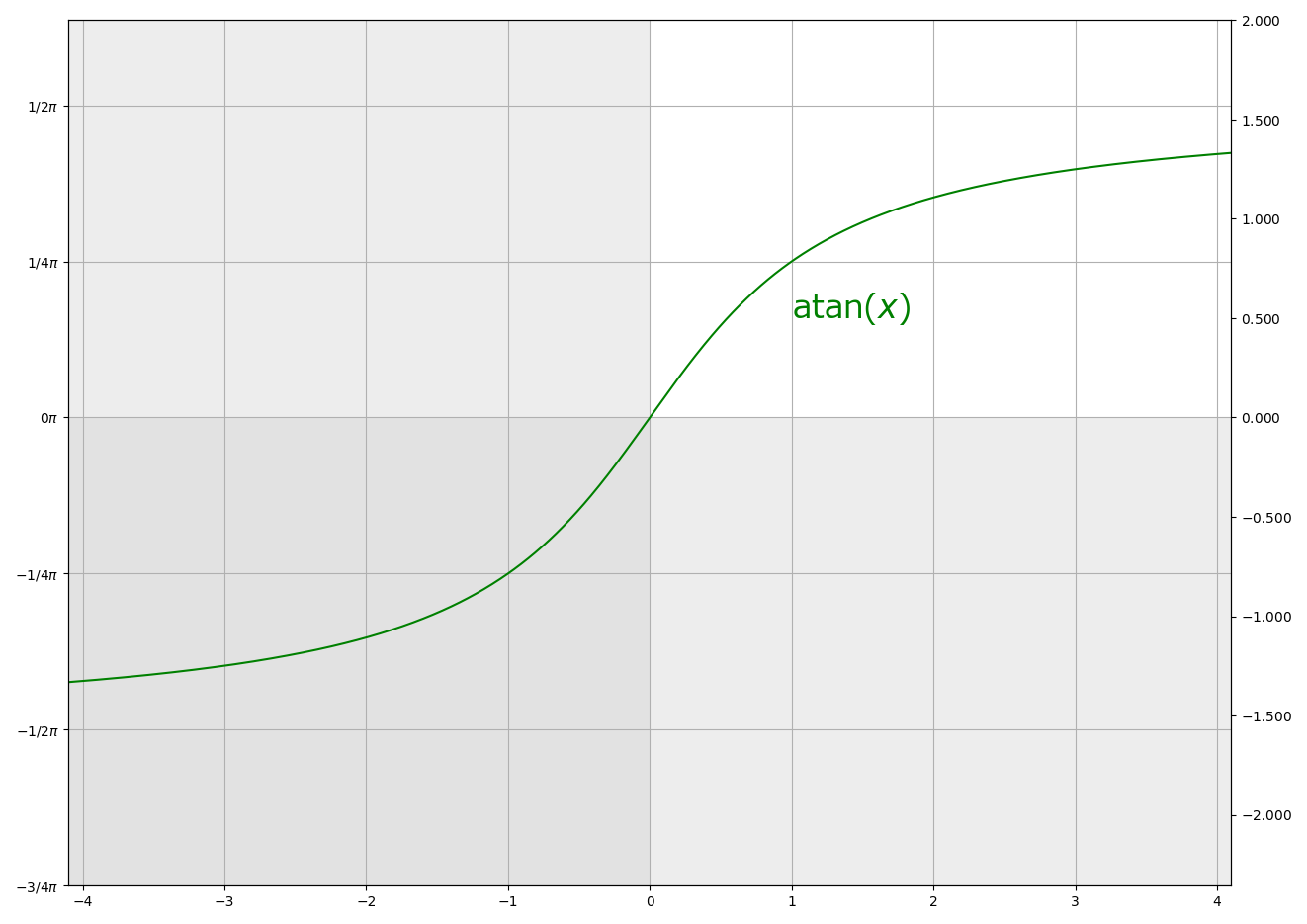
atan(x)

Compute arctangent of x.

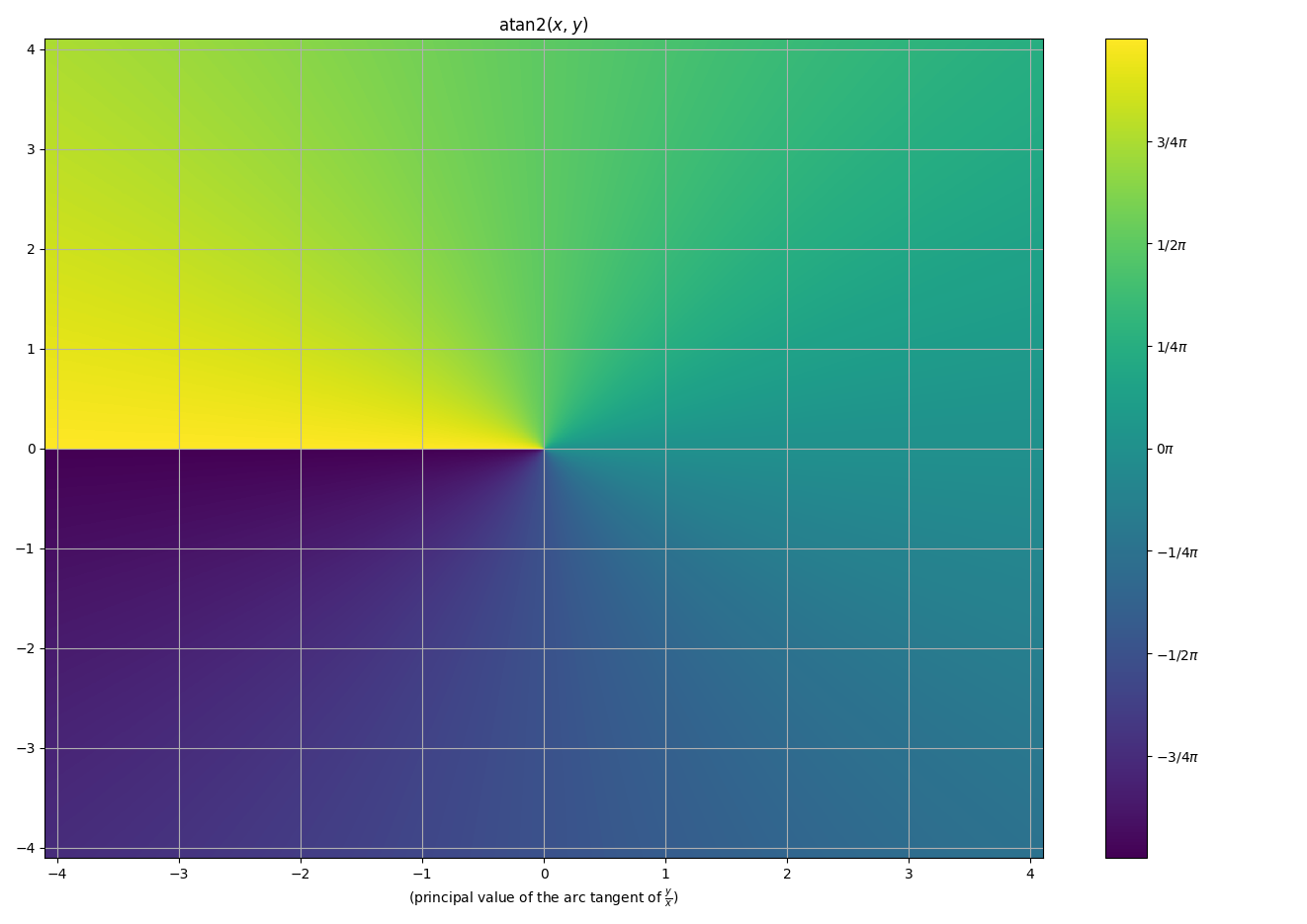
atan2(x, y)

Compute principal value of the arc tangent of y/x.

../_images/expression_itrig1_graph.png ../_images/expression_itrig2_graph.png ../_images/expression_itrig3_graph.png 
[me@host: ~]$ ffplay -f lavfi "aevalsrc='0.25 * acos(mod(t, 1)) * sin(440 * 2 * PI * t)'"

Hyperbolic functions

Official documentation says:

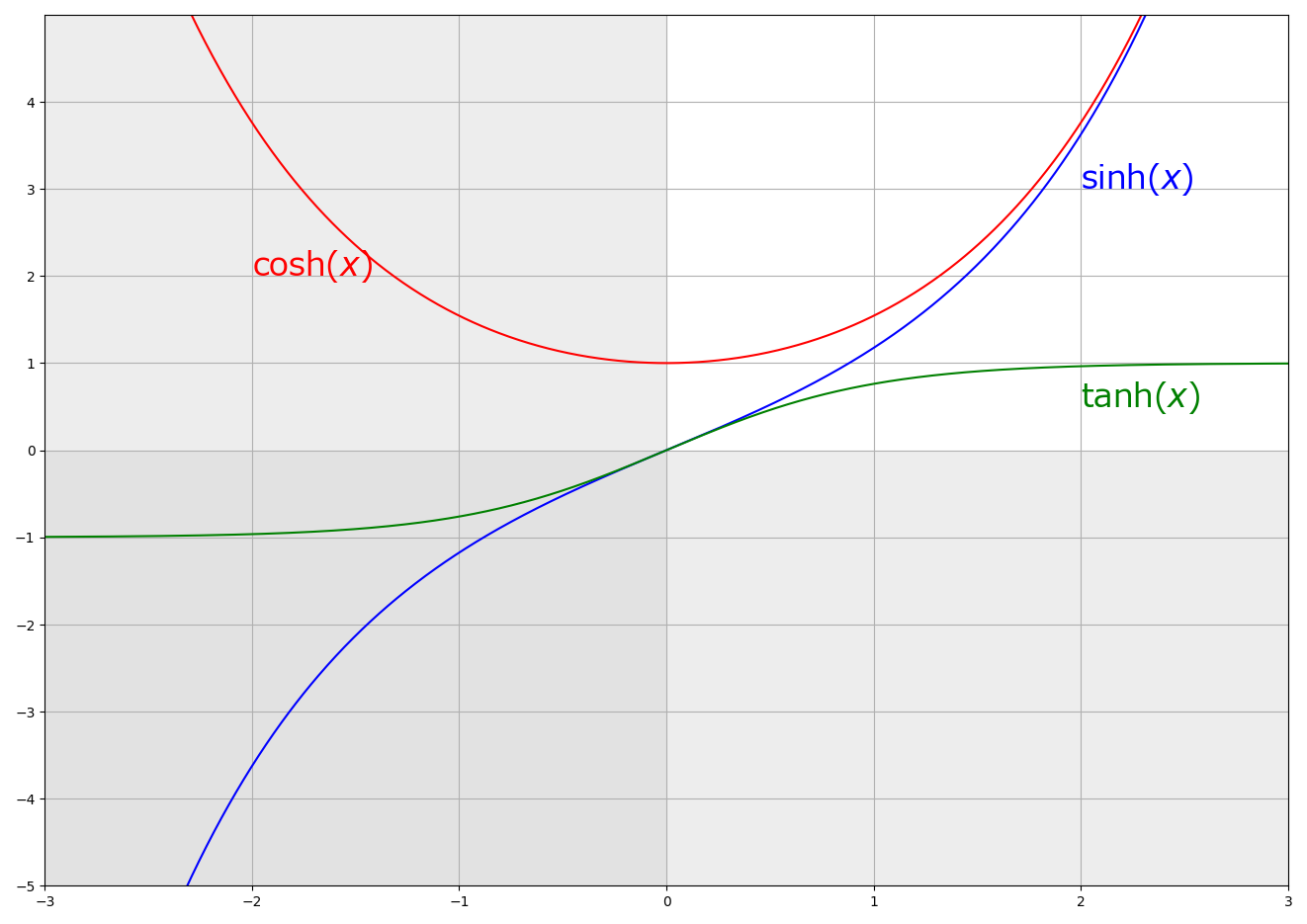
cosh(x)

Compute hyperbolic cosine of x.

sinh(x)

Compute hyperbolic sine of x.

tanh(x)

Compute hyperbolic tangent of x.

../_images/expression_hyperb_graph.png 
[me@host: ~]$ ffplay -f lavfi "aevalsrc='0.25 * tanh(mod(t, 1)) * sin(440 * 2 * PI * t)'"

sgn(x)

Official documentation says:

sgn(x)

Compute sign of x.

[me@host: ~]$ ffplay video.mkv -vf "eq=contrast=sgn(sin(100 * t)) * 2.0:eval=frame"

clip(x, min, max), max(x, y), min(x, y)

Official documentation says:

clip(x, min, max)

Return the value of x clipped between min and max.

max(x, y)

Return the maximum between x and y.

min(x, y)

Return the minimum between x and y.

#! /bin/sh
ffmpeg -i video.mkv -vf "
    color=blue@0.3:size=150x150,loop=-1:size=2[m];
    [0:v][m]
        overlay='
            x=W * clip(1 / 2 * (1 - cos(4 * t)), 1 / 4, 3 / 4):
            y=H * clip(1 / 2 * (1 - cos(8 * t)), 1 / 4, 3 / 4)'" \
    -f matroska - | ffplay -

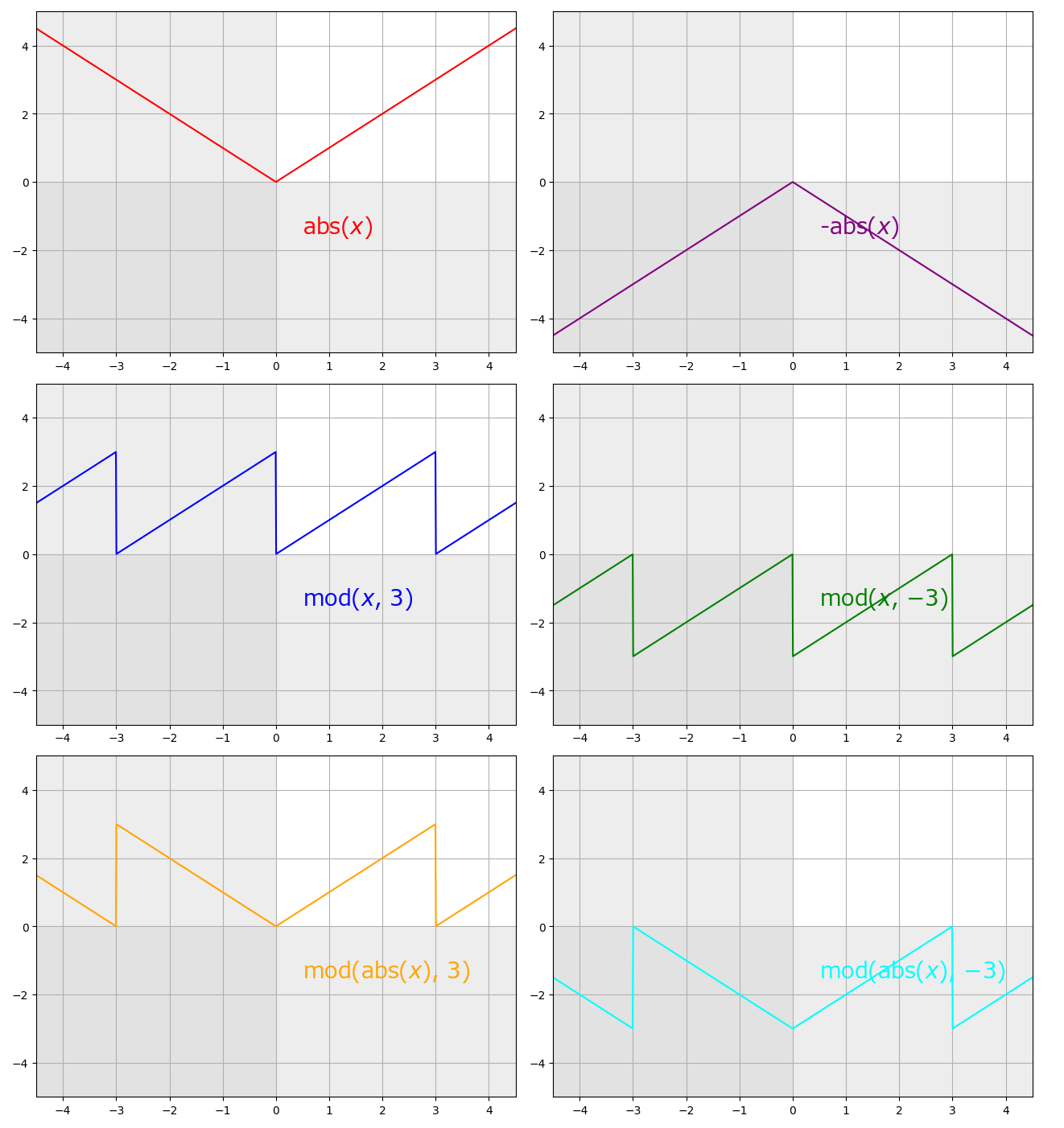
abs(x), mod(x, y)

Official documentation says:

abs(x)

Compute absolute value of x.

mod(x, y)

Compute the remainder of division of x by y.

../_images/expression_mod_graph.png 
[me@host: ~]$ ffplay -f lavfi "aevalsrc='0.25 * abs(1 - mod(t, 2)) * sin(440 * 2 * PI * t)'"

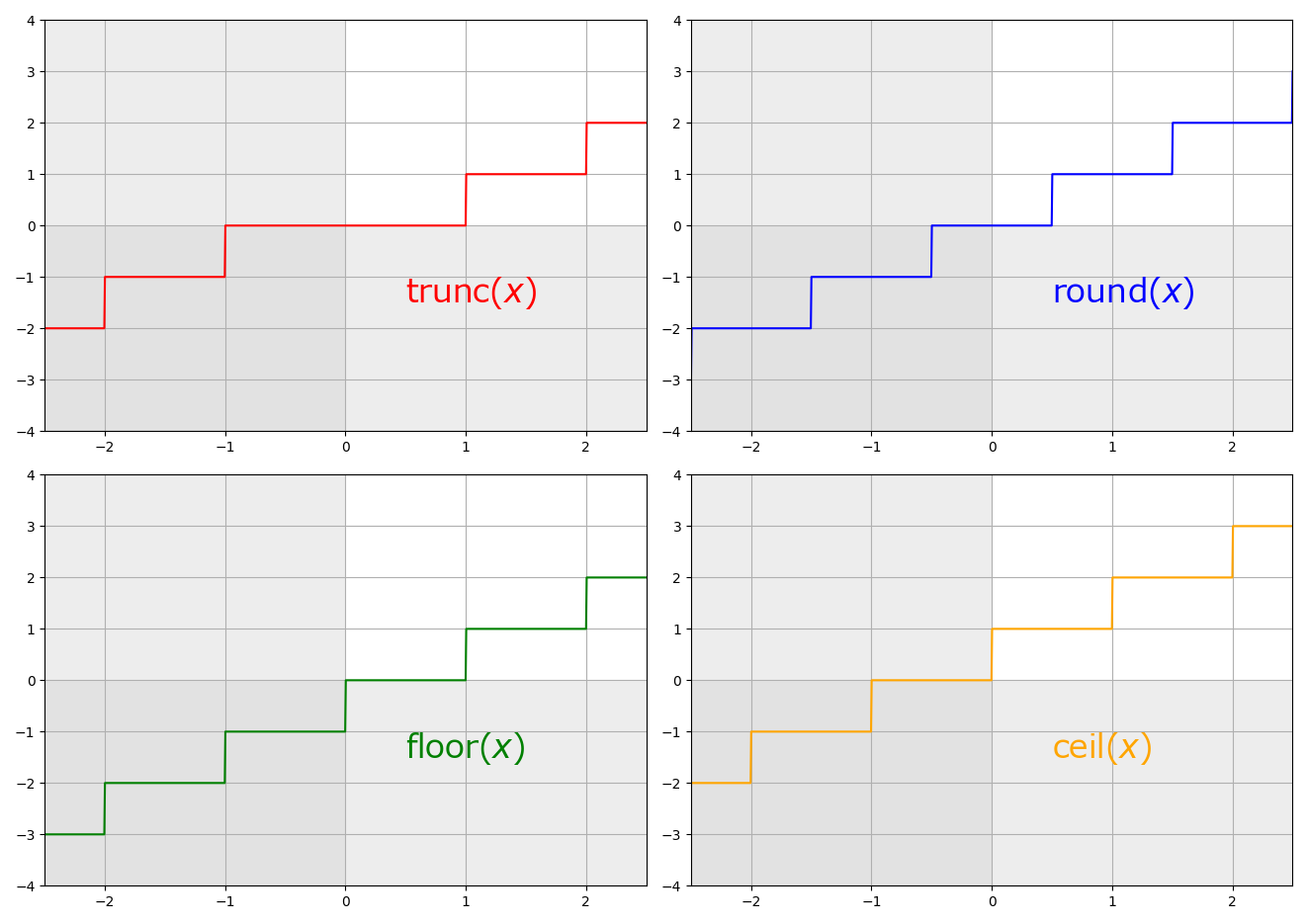
ceil(expr), floor(expr), trunc(expr), round(expr)

Official documentation says:

ceil(expr)

Round the value of expression expr upwards to the nearest integer. For example, ceil(1.5) is 2.0.

floor(expr)

Round the value of expression expr downwards to the nearest integer. For example, floor(-1.5) is -2.0.

trunc(expr)

Round the value of expression expr towards zero to the nearest integer. For example, trunc(-1.5) is -1.0.

round(expr)

Round the value of expression expr to the nearest integer. For example, round(1.5) is 2.0.

../_images/expression_trunc_graph.png

Note

Note that the behavior of the “round” function may differ from that of your favorite programming language (ex. “round” of Python).

[me@host: ~]$ ffplay -f lavfi "aevalsrc='0.05 * (mod(round(t), 10)) * sin(440 * 2 * PI * t)'"

lerp(x, y, z)

Official documentation says:

lerp(x, y, z)

Return linear interpolation between x and y by amount of z.

It’s literally the simplest linear interpolation, so you won’t find this essential. In some cases, you can write expression slightly smarter, as shown below:

[me@host: ~]$ ffplay -vf "crop='960:540:((iw - 0) * cos(t)):((ih - 0) * sin(t))'" video.mkv
[me@host: ~]$ ffplay -vf "crop='960:540:lerp(0, iw, cos(t)):lerp(0, ih, sin(t))'" video.mkv

gcd(x, y)

Official documentation says:

gcd(x, y)

Return the greatest common divisor of x and y. If both x and y are 0 or either or both are less than zero then behavior is undefined.

[me@host: ~]$ # the greatest common divisor of 720 and 1080 is 360.
[me@host: ~]$ ffplay -vf "scale=-1:'gcd(720, 1080)'" video.mkv
see also

lcm(x, y)

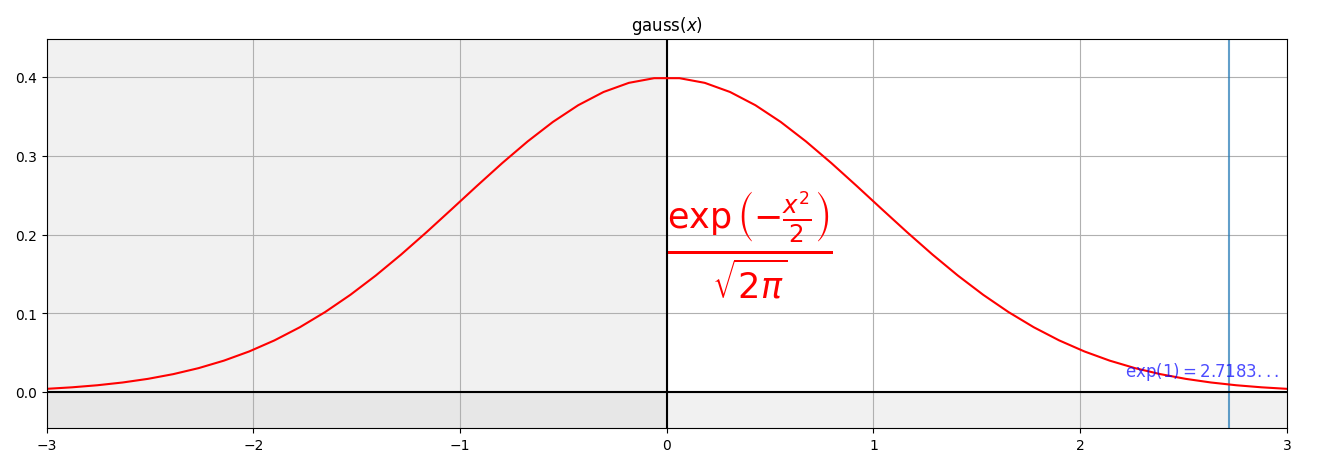
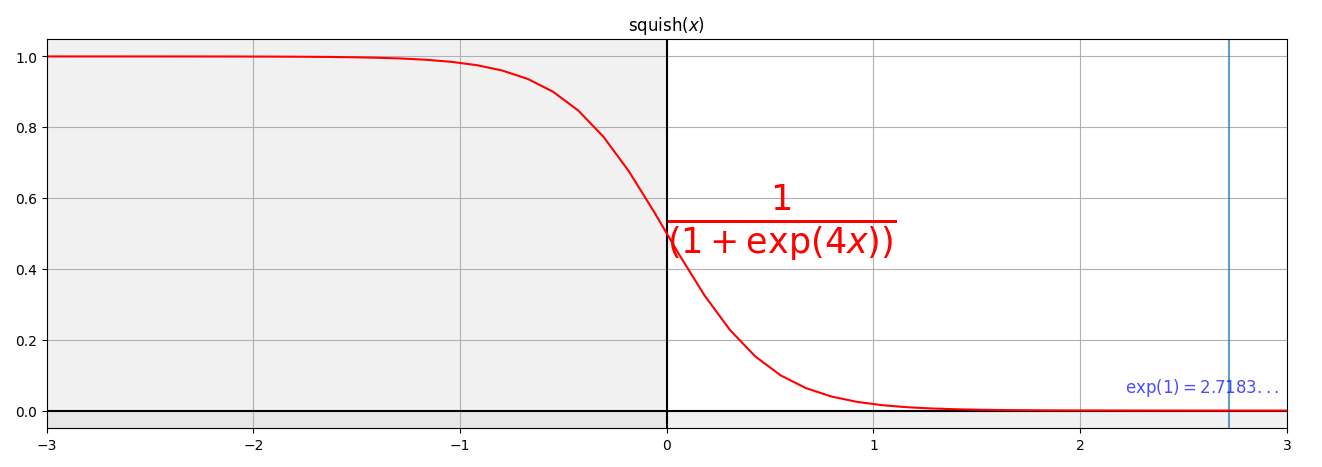
exp(x), gauss(x), squish(x)

Official documentation says:

exp(x)

Compute exponential of x (with base e, the Euler’s number).

../_images/expression_exp_graph.png

gauss(x)

Compute Gauss function of x, corresponding to \(\exp(-x^{2}/2) / \sqrt{2 \pi}\).

../_images/expression_gauss_graph.png

squish(x)

Compute expression \(1 / (1 + \exp(4x))\).

../_images/expression_squish_graph.png 
[me@host: ~]$ ffplay -f lavfi "aevalsrc='0.5 * gauss(mod(t, 3) - 1.5) * sin(220 * 2 * PI * t)'"
[me@host: ~]$ ffplay -f lavfi "aevalsrc='0.5 * squish(mod(t, 3) - 1.5) * sin(220 * 2 * PI * t)'"

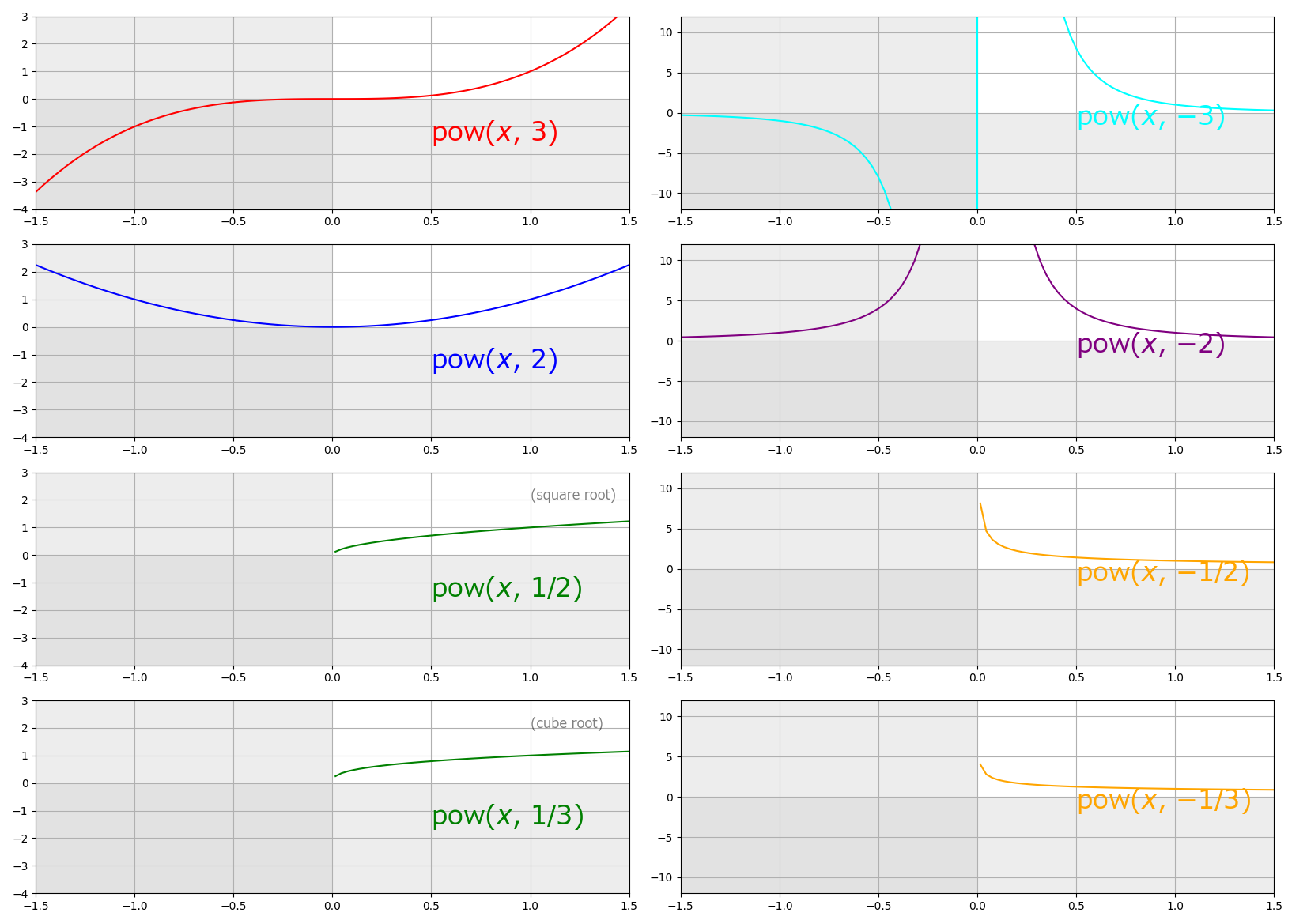
pow(x, y), sqrt(expr), hypot(x, y), log(x)

Official documentation says:

pow(x, y)

Compute the power of x elevated y, it is equivalent to (x)^(y).

../_images/expression_pow_graph.png

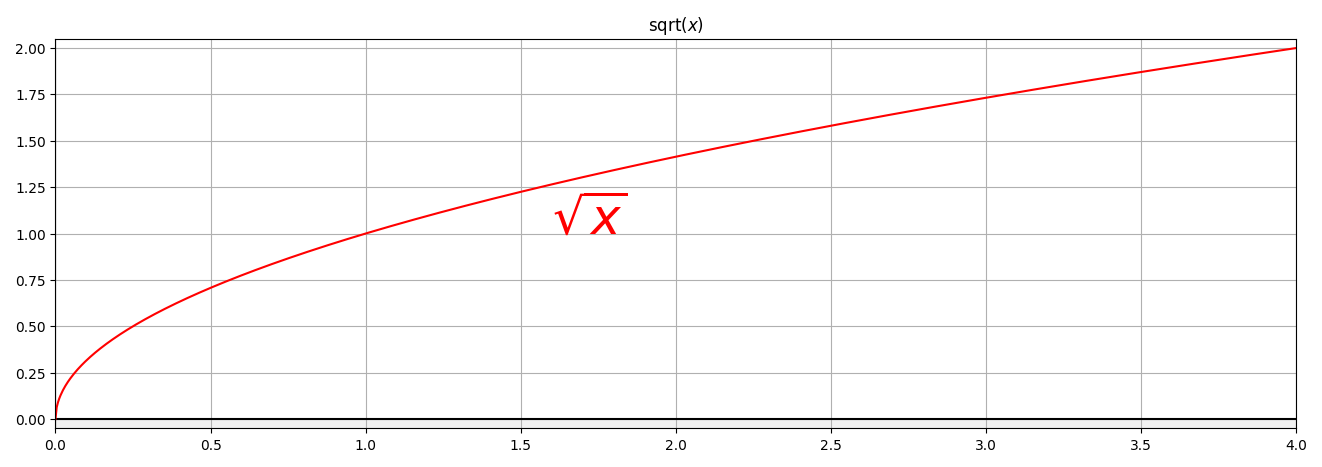
sqrt(expr)

Compute the square root of expr. This is equivalent to (expr)^.5.

../_images/expression_sqrt_graph.png

hypot(x, y)

This function is similar to the C function with the same name; it returns sqrt(x*x + y*y), the length of the hypotenuse of a right triangle with sides of length x and y, or the distance of the point (x, y) from the origin.

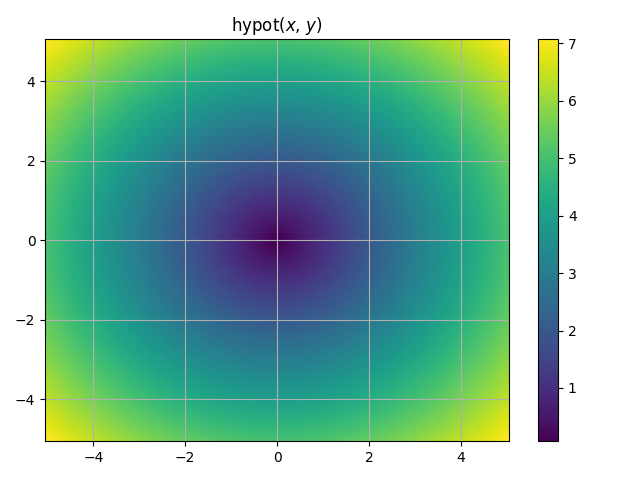
../_images/expression_hypot_graph.png

log(x)

Compute natural logarithm of x.

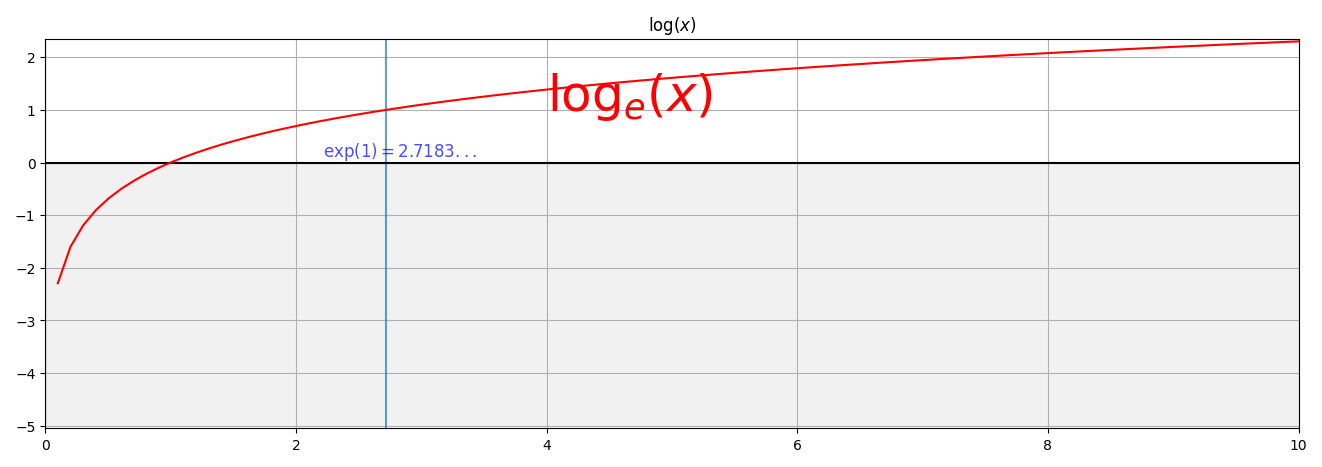
../_images/expression_log_graph.png ../_images/expression_log2_graph.png 
[me@host: ~]$ ffplay -f lavfi "aevalsrc='0.1 * sin((pow(2, ((floor(2 * t) + 69) - 69) / 12.) * 440) * 2 * PI * t)'"

random(x)

Official documentation says:

random(x)

Return a pseudo random value between 0.0 and 1.0. x is the index of the internal variable which will be used to save the seed/state.

[me@host: ~]$ ffplay -vf "crop=100:100:'(iw - ow) * random(0):(ih - oh) * random(0)'" video.mkv

st(var, expr), ld(var)

Official documentation says:

ld(var)

Load the value of the internal variable with number var, which was previously stored with st(var, expr). The function returns the loaded value.

st(var, expr)

Store the value of the expression expr in an internal variable. var specifies the number of the variable where to store the value, and it is a value ranging from 0 to 9. The function returns the value stored in the internal variable. Note, Variables are currently not shared between expressions.

For example:

#! /bin/sh
ffplay -f lavfi "
aevalsrc='
    0.125 / (st(0, mod(t, 1)) * ld(0)) * sin(440 * 2 * PI * t)
'"

It would be easier to maintain the st statement and the statement that uses ld separately. The following is exactly the same:

#! /bin/sh
ffplay -f lavfi "
aevalsrc='
    st(0, mod(t, 1));
    0.125 / (ld(0) * ld(0)) * sin(440 * 2 * PI * t)
'"

The following picture shows the relationship between st and ld:

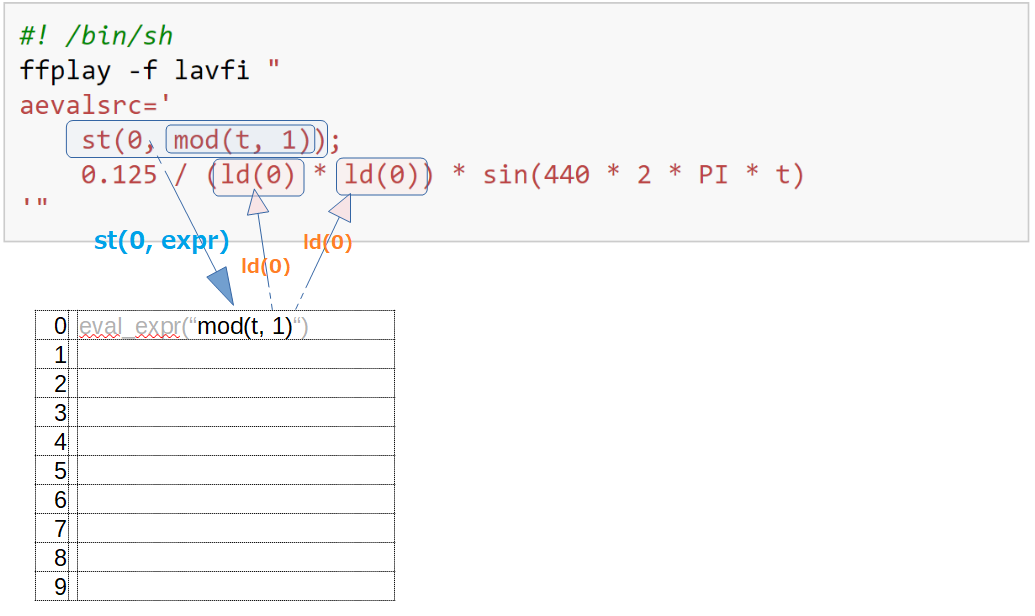
../_images/st_ld_image.png

You can use up to 9 variables, so you can write something a little more complicated like this:

#! /bin/sh
ffplay -f lavfi "
aevalsrc='
    st(0, 2 * PI * t);
    st(1, mod(t, 1) / 4);
    st(2, mod(t, 3) / 12);
    (ld(1) * sin(220 * ld(0)) + ld(2) * sin(440 * ld(0)))
'"

while(cond, expr)

Official documentation says:

while(cond, expr)

Evaluate expression expr while the expression cond is non-zero, and returns the value of the last expr evaluation, or NAN if cond was always false.

Example of “Start with 5000 and repeat dividing by 2 until it falls below 500”:

#! /bin/sh
# For example, imagine the following code in the Python language:
# ---------------------------------------------------------------
# d = 5000
# while d > 500:  # cond
#     d /= 2      # expr
# ---------------------------------------------------------------
ffplay -f lavfi "
aevalsrc='
    st(0, 5000);
    while(gt(ld(0), 500), st(0, ld(0) / 2));
    0.5 * sin(ld(0) * 2 * PI * t)
'"

factorial(n):

\[n! = n \times (n - 1) \times \cdots \times 1\]
#! /bin/sh
# For example, imagine the following code in the Python language:
# ---------------------------------------------------------------
# k = 4
# v = 1
# while k > 1:  # cond
#     v *= k    # expr
#     k -= 1    # ; expr
# ---------------------------------------------------------------
# 4! = 4 * 3 * 2 = 24
ffplay -f lavfi "
aevalsrc='
    st(0, 4);
    st(1, 1);
    while(
        gt(ld(0), 1),
            st(1, ld(0) * ld(1))
            ; st(0, ld(0) - 1)
    );
    print(ld(1))'"

root(expr, max)

Official documentation says:

root(expr, max)

Find an input value for which the function represented by expr with argument ld(0) is 0 in the interval 0 .. max.

The expression in expr must denote a continuous function or the result is undefined.

ld(0) is used to represent the function input value, which means that the given expression will be evaluated multiple times with various input values that the expression can access through ld(0). When the expression evaluates to 0 then the corresponding input value will be returned.

If expr is root(sin(ld(0)) - 1, 2), root will return 0.5 * PI:

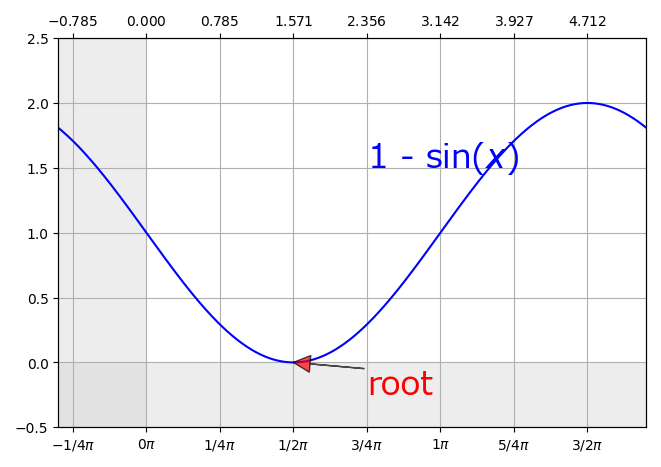
../_images/expression_root_graph_01.png

, if expr is root(sin(ld(0)) + 6 + sin(ld(0) / 12) - log(ld(0)), 100), root will return 60.97:

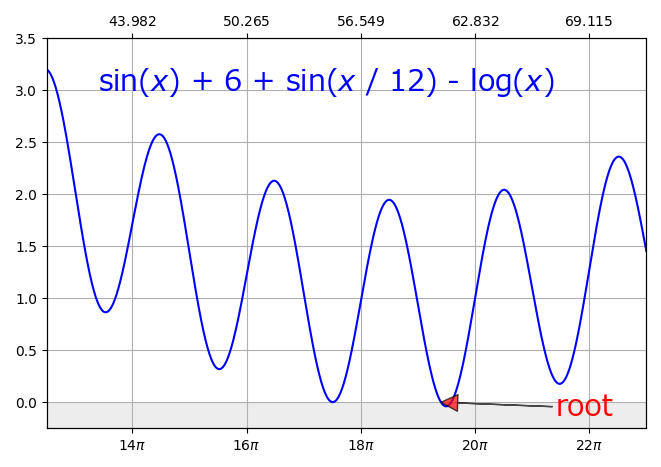
../_images/expression_root_graph_02.png

, if expr is root(log(ld(0)) - 3, 100), root will return 20.085537:

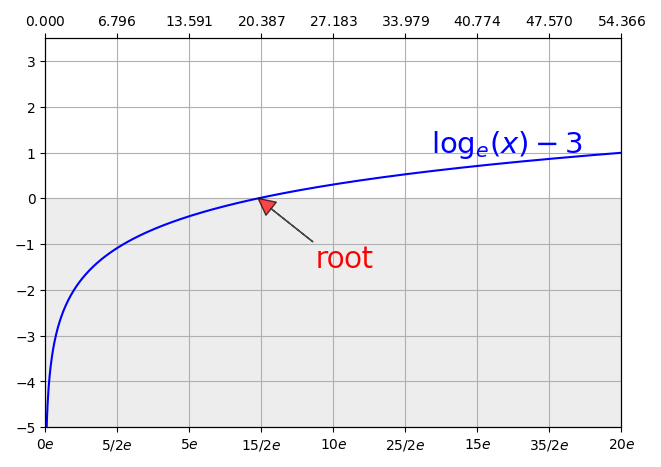
../_images/expression_root_graph_03.png

taylor(expr, x), taylor(expr, x, id)

Official documentation says:

Evaluate a Taylor series at x, given an expression representing the ld(id)-th derivative of a function at 0.

When the series does not converge the result is undefined.

ld(id) is used to represent the derivative order in expr, which means that the given expression will be evaluated multiple times with various input values that the expression can access through ld(id). If id is not specified then 0 is assumed.

Note, when you have the derivatives at y instead of 0, taylor(expr, x-y) can be used.

What this function does is probably:

\[\textrm{expr}_{0} + \textrm{expr}_{1}x + \frac{\textrm{expr}_{2}}{2!}x^{2} + \cdots + \frac{\textrm{expr}_{n}}{n!}x^{n} + \cdots\]

if so, I don’t think it is usefull at all. For example, this cannot be used to approximate the “sinh” function, it is because control of “n” is not allowed. (If not my misunderstanding.)

the International System unit prefixes

Official documentation says:

The evaluator also recognizes the International System unit prefixes. If i is appended after the prefix, binary prefixes are used, which are based on powers of 1024 instead of powers of 1000. The B postfix multiplies the value by 8, and can be appended after a unit prefix or used alone. This allows using for example KB, MiB, G and B as number postfix.

prefix

if i is appended

y

\(10^{-24}\)

\(2^{-80}\)

z

\(10^{-21}\)

\(2^{-70}\)

a

\(10^{-18}\)

\(2^{-60}\)

f

\(10^{-15}\)

\(2^{-50}\)

p

\(10^{-12}\)

\(2^{-40}\)

n

\(10^{-9}\)

\(2^{-30}\)

u

\(10^{-6}\)

\(2^{-20}\)

m

\(10^{-3}\)

\(2^{-10}\)

c

\(10^{-2}\)

d

\(10^{-1}\)

h

\(10^{2}\)

k or K

\(10^{3}\)

\(2^{10}\)

M

\(10^{6}\)

\(2^{20}\)

G

\(10^{9}\)

\(2^{30}\)

T

\(10^{12}\)

\(2^{40}\)

P

\(10^{15}\)

\(2^{40}\)

E

\(10^{18}\)

\(2^{50}\)

Z

\(10^{21}\)

\(2^{60}\)

Y

\(10^{24}\)

\(2^{70}\)

 
[me@host: ~]$ ffplay -f lavfi "aevalsrc='sin(2k * 2 * PI * t)'"